How to Master L’Hôpital’s Rule: 7 Essential Principles for Calculus Success
Have your students ever been puzzled by calculus limits that seem impossible to solve?
Imagine effortlessly tackling these challenging calculus problems with a clear, structured approach to mastering L’Hôpital’s rule in calculus.
As an experienced educator, I’ve guided many students through mastering difficult concepts and advanced differentiation methods.
L’Hôpital’s rule can transform how your students approach limits and indeterminate forms in calculus, enhancing their math problem-solving techniques.
In this blog, you’ll find a step-by-step guide to teaching L’Hôpital’s rule for evaluating complex limits. We will cover common student struggles with convergence and divergence, practical solutions, and effective teaching strategies for calculus exam preparation.
Let’s dive into mastering L’Hôpital’s rule in calculus and explore its application in mathematical analysis techniques.

Understanding the Struggles with Indeterminate Forms
When students encounter indeterminate forms in calculus limits, they often feel overwhelmed and confused. These forms, such as 0/0 or ∞/∞, can make limits seem unsolvable, challenging students’ mathematical analysis techniques.
In my experience, students frequently struggle to recognize when L’Hôpital’s rule applies. This struggle can lead to a lack of confidence and frustration when evaluating complex limits. Mastering L’Hôpital’s rule in calculus is essential for overcoming these difficulties.
Moreover, these difficulties can impact their overall calculus performance. They might find themselves stuck on problems involving convergence and divergence or asymptotes and infinite limits, which hinders their academic progress and calculus exam preparation.
Mastering these techniques is crucial not just for passing exams, but for real-world applications in scientific and engineering fields. Developing strong math problem-solving techniques and advanced differentiation methods is key to success in calculus and beyond.
A Roadmap to Mastering L’Hôpital’s Rule
Overcoming this challenge in mastering L’Hôpital’s rule calculus requires a few key steps. Here are the main areas to focus on to make progress in evaluating complex limits:
- Understand indeterminate forms 0/0 and ∞/∞: Learn definitions and recognize these forms in calculus limits.
- Practice identifying applicable limit scenarios: Develop a checklist for when L’Hôpital’s rule applies in mathematical analysis techniques.
- Master differentiation techniques for complex functions: Focus on advanced differentiation methods for derivative application.
- Apply L’Hôpital’s rule to exponential functions: Assign targeted problems involving exponential functions and asymptotes.
- Solve problems with limits as x approaches infinity: Use graphing tools to visualize these infinite limits.
- Create visual aids to represent the rule’s concept: Develop infographics and animations for better understanding of convergence and divergence.
- Utilize proof-based approaches for deeper understanding: Introduce proof-based problems in advanced classes for mastering L’Hôpital’s rule calculus.
Let’s dive into these math problem-solving techniques for calculus exam preparation!
1: Understand indeterminate forms 0/0 and ∞/∞
Understanding indeterminate forms is essential for mastering L’Hôpital’s rule calculus and solving complex calculus problems, particularly when evaluating complex limits.
Actionable Steps:
- Define indeterminate forms clearly: Start by providing precise definitions of 0/0 and ∞/∞, crucial for calculus limits.
- Use visual aids: Incorporate graphs and diagrams to help students identify these forms in various problems, aiding in mathematical analysis techniques.
- Practice identifying forms: Create a set of practice problems focused specifically on recognizing indeterminate forms, enhancing math problem-solving techniques.
Key concepts to grasp:
- Definition of indeterminate forms
- Common types of indeterminate forms in calculus
- Importance in calculus problem-solving and derivative application
Explanation: Recognizing indeterminate forms is the first step in applying L’Hôpital’s rule effectively. By using clear definitions and visual aids, you can make these concepts more accessible for mastering L’Hôpital’s rule calculus.
Practice problems reinforce learning and help students gain confidence in advanced differentiation methods. For additional resources, check out this detailed explanation on L’Hôpital’s rule.
Mastering these initial steps will set a strong foundation for more advanced techniques in calculus exam preparation, including understanding convergence and divergence, and analyzing asymptotes and infinite limits.
2: Practice identifying applicable limit scenarios
Recognizing when to apply L’Hôpital’s rule is crucial for mastering L’Hôpital’s rule calculus and solving complex calculus problems effectively.
Actionable Steps:
- Develop a checklist: Create a clear and concise checklist that outlines the conditions under which L’Hôpital’s rule can be applied, focusing on indeterminate forms and evaluating complex limits.
- Organize peer study groups: Encourage students to form study groups to solve limit problems collaboratively and discuss their reasoning, enhancing their calculus exam preparation.
- Use software tools: Implement software tools that generate random limit problems for practice, enhancing student exposure to various scenarios involving calculus limits and asymptotes and infinite limits.
Explanation: These steps are essential because they provide students with structured guidance and collaborative opportunities for mastering L’Hôpital’s rule calculus.
A checklist helps them quickly determine if L’Hôpital’s rule is applicable, while peer study groups foster a deeper understanding of advanced differentiation methods through shared problem-solving.
For additional practice problems, consider using resources from Fiveable.
These strategies will help students gain confidence in identifying when to use L’Hôpital’s rule, leading to better math problem-solving techniques and mathematical analysis techniques.

3: Master differentiation techniques for complex functions
Mastering differentiation techniques for complex functions is crucial to applying L’Hôpital’s rule effectively in calculus, especially when dealing with indeterminate forms and evaluating complex limits.
Actionable Steps:
- Conduct focused workshops: Organize sessions on advanced differentiation methods to deepen understanding of mastering L’Hôpital’s rule in calculus.
- Schedule one-on-one tutoring: Provide personalized instruction to address individual student needs in calculus limits and derivative applications.
- Utilize online resources: Leverage interactive tutorials for additional practice and reinforcement of math problem-solving techniques.
Explanation: These steps are essential for building a solid foundation in differentiation, a key skill for mastering L’Hôpital’s rule and analyzing convergence and divergence in calculus.
Workshops and tutoring offer targeted learning, while online resources provide continuous practice for evaluating complex limits and understanding asymptotes and infinite limits.
For more tips on differentiation techniques, explore this resource at iTransfer.
By implementing these strategies, students will enhance their calculus skills, improve their mathematical analysis techniques, and gain confidence in calculus exam preparation.

4: Apply L’Hôpital’s rule to exponential functions
Applying L’Hôpital’s rule to exponential functions is crucial for mastering L’Hôpital’s rule in calculus and solving advanced calculus problems, especially when evaluating complex limits.
Actionable Steps:
- Introduce exponential functions thoroughly: Use engaging lectures to explain exponential functions and their properties in relation to indeterminate forms and asymptotes.
- Assign targeted homework problems: Design assignments that specifically involve applying L’Hôpital’s rule to exponential functions for practice in advanced differentiation methods.
- Encourage peer presentations: Have students present their solutions in class for peer feedback and discussion, focusing on calculus limits and convergence.
Benefits of mastering exponential functions:
- Enhanced math problem-solving techniques
- Better understanding of real-world applications of calculus
- Improved performance in advanced calculus courses and exams
Explanation: These steps help build a deep understanding of exponential functions and how to apply L’Hôpital’s rule effectively in mathematical analysis.
Engaging lectures and targeted homework reinforce learning, while peer presentations foster collaborative learning in mastering L’Hôpital’s rule calculus.
For more on mastering these techniques, explore this comprehensive guide on L’Hôpital’s rule.
Implementing these strategies will enhance students’ problem-solving skills and confidence in calculus, particularly in dealing with indeterminate forms and infinite limits.

5: Solve problems with limits as x approaches infinity
Understanding how to solve problems involving limits as x approaches infinity is essential for mastering advanced calculus concepts, including mastering L’Hôpital’s rule calculus.
Actionable Steps:
- Create progressively challenging problems: Design a series of problems that increase in difficulty to help students build their skills gradually, focusing on calculus limits and indeterminate forms.
- Use graphing tools: Integrate graphing software to visualize the behavior of functions as x approaches infinity, aiding in understanding asymptotes and infinite limits.
- Host Q&A sessions: Organize regular sessions to address specific student questions and reinforce understanding of advanced differentiation methods and evaluating complex limits.
Explanation: These steps are crucial because they provide a structured approach to mastering limits at infinity and L’Hôpital’s rule calculus.
Gradual problem-solving builds confidence, while visual tools enhance comprehension of convergence and divergence. Regular Q&A sessions ensure that students’ concerns about mathematical analysis techniques are addressed promptly.
For additional practice and resources on mastering L’Hôpital’s rule calculus, consider exploring this guide on L’Hôpital’s rule.
Implementing these strategies will help students tackle complex calculus problems with greater ease and improve their calculus exam preparation.

6: Create visual aids to represent the rule’s concept
Creating visual aids is essential for making L’Hôpital’s rule more accessible and easier to understand for students mastering L’Hôpital’s rule calculus.
Actionable Steps:
- Develop infographics: Break down the steps of applying L’Hôpital’s rule into simple, visual representations, focusing on indeterminate forms and derivative applications.
- Create animations and videos: Use dynamic tools to illustrate complex concepts in calculus limits, making them more engaging.
- Encourage student-made aids: Have students create their own visual aids as a learning exercise to reinforce advanced differentiation methods.
Explanation: These steps are crucial because they transform abstract concepts into tangible visuals, aiding comprehension of mathematical analysis techniques.
Infographics and animations simplify learning, while student-created aids reinforce understanding of convergence and divergence in calculus.
For more on creating effective visual aids, explore this resource at USA.edu.
Implementing these strategies will help students grasp L’Hôpital’s rule more effectively and boost their confidence in calculus exam preparation and evaluating complex limits.
7: Utilize proof-based approaches for deeper understanding
Using proof-based approaches deepens students’ understanding of L’Hôpital’s rule and its applications in calculus limits and indeterminate forms.
Actionable Steps:
- Introduce proof-based problems: Begin incorporating proof-based problems into advanced calculus classes to challenge students in mastering L’Hôpital’s rule calculus.
- Facilitate theoretical seminars: Organize seminars to discuss the theoretical foundations of L’Hôpital’s rule, encouraging deeper insight into advanced differentiation methods.
- Assign research projects: Have students undertake projects that involve proving L’Hôpital’s rule in various contexts to solidify their comprehension of mathematical analysis techniques.
Key benefits of proof-based learning:
- Develops critical thinking skills for evaluating complex limits
- Enhances mathematical reasoning abilities in calculus
- Prepares students for advanced mathematical studies and calculus exam preparation
Explanation: These steps are vital for fostering a deeper understanding of L’Hôpital’s rule. Proof-based problems and theoretical discussions help students see the underlying logic, enhancing their math problem-solving techniques.
Research projects promote independent learning and critical thinking in mastering L’Hôpital’s rule calculus. For additional resources, consider exploring this detailed guide on L’Hôpital’s rule.
Incorporating these strategies will help students grasp complex calculus concepts more thoroughly, including convergence and divergence, asymptotes and infinite limits, and derivative applications.

Partner with Alleo to Master L’Hôpital’s Rule
We’ve explored the challenges of mastering L’Hôpital’s rule calculus and the steps to overcome them. But did you know you can work directly with Alleo to make this journey easier and faster, especially when dealing with complex limits and indeterminate forms?
With Alleo, you’ll get tailored coaching support for advanced differentiation methods and mathematical analysis techniques. Our AI coach provides full coaching sessions just like a human coach, helping you with calculus limits and derivative applications.
Start by setting up your account and creating a personalized plan for mastering L’Hôpital’s rule calculus. Alleo’s coach will follow up on your progress and handle changes, assisting you with convergence and divergence concepts.
You’ll receive regular text and push notifications to keep you accountable, perfect for your calculus exam preparation and improving your math problem-solving techniques.
Ready to get started for free and enhance your skills in evaluating complex limits and understanding asymptotes and infinite limits? Let me show you how!
Step 1: Logging In or Creating an Account
To begin mastering L’Hôpital’s rule with our AI coach, simply Log in to your account or create a new one to access personalized coaching and support tailored to your calculus learning journey.

Step 2: Choose “Building better habits and routines”
Select “Building better habits and routines” to develop a structured approach for mastering L’Hôpital’s rule and other complex calculus concepts, enabling you to establish consistent study practices and problem-solving techniques.

Step 3: Select “Career” as Your Focus Area
Choose “Career” as your focus area to enhance your calculus skills and problem-solving abilities, which are crucial for success in STEM fields and can significantly boost your professional prospects.

Step 4: Starting a Coaching Session
Begin your journey with Alleo by scheduling an initial intake session, where our AI coach will help you create a personalized plan to master L’Hôpital’s rule and other challenging calculus concepts.

Step 5: Viewing and Managing Goals After the Session
After your coaching session on L’Hôpital’s rule, check the Alleo app’s home page to review and manage the goals you discussed, helping you stay on track with your calculus learning journey.
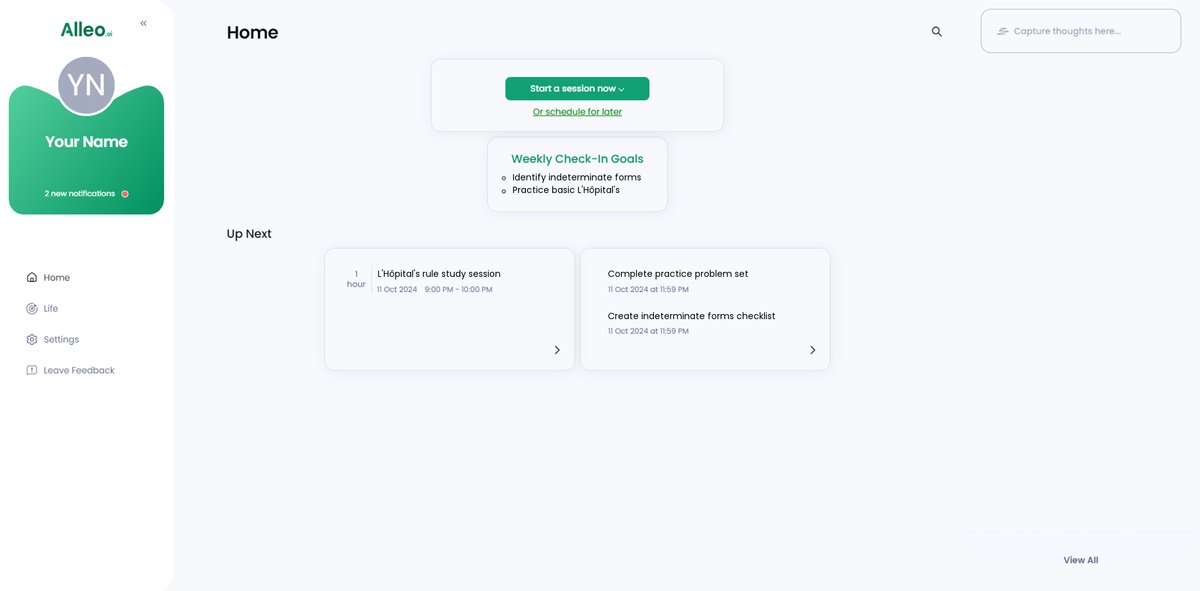
Step 6: Adding events to your calendar or app
Use the calendar and task features in the Alleo app to schedule and track your progress on L’Hôpital’s rule problems, helping you stay organized and motivated as you work through challenging calculus concepts.
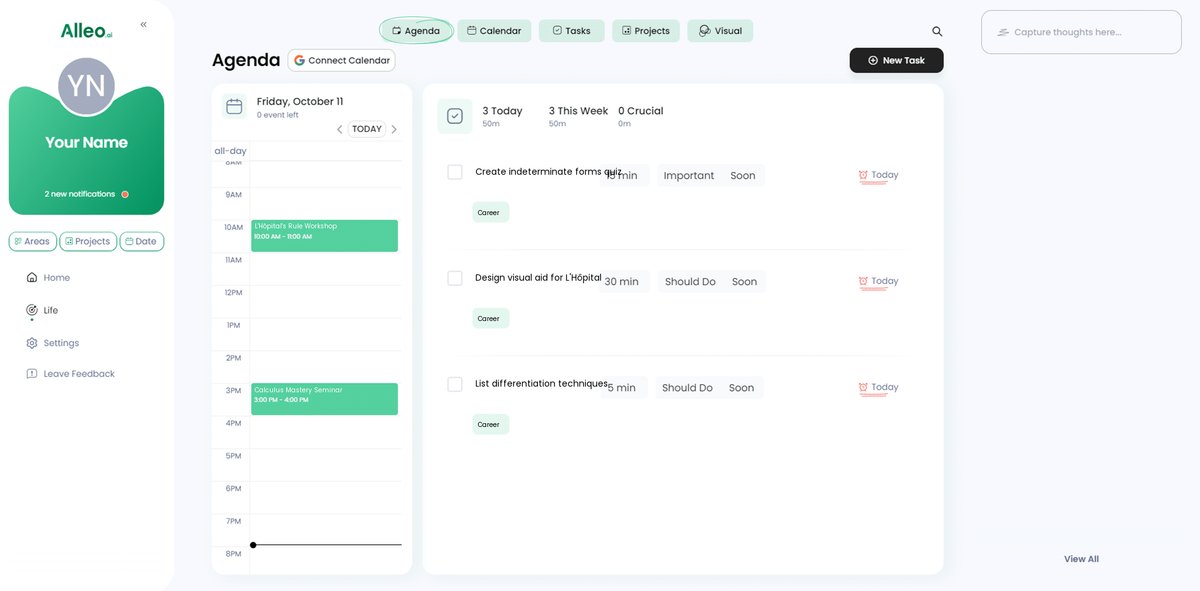
Putting It All Together: Mastering L’Hôpital’s Rule
We’ve explored the steps to mastering L’Hôpital’s rule calculus, from understanding indeterminate forms to using proof-based approaches in mathematical analysis techniques.
I know it can be challenging, but with structured guidance, you and your students can overcome these obstacles in evaluating complex limits and advanced differentiation methods.
Remember, consistent practice and utilizing visual aids can make a huge difference in mastering calculus limits and convergence and divergence concepts.
Don’t forget to leverage personalized support from Alleo for your calculus exam preparation.
With our AI coach, you’ll receive tailored feedback and stay on track with your learning journey in math problem-solving techniques.
Start your free trial today and transform your approach to mastering L’Hôpital’s rule calculus!
You’ve got this!