Master L’Hôpital’s Rule: 6 Fundamental Steps to Simplify Complex Algebra in Calculus
Are your students struggling with simplifying algebra for L’Hôpital’s rule in calculus? This technique for evaluating indeterminate forms can be challenging when complex algebraic manipulation is required.
As an educator, I’ve seen many students face this challenge. They often get stuck on algebraic manipulations, making it difficult to apply L’Hôpital’s rule effectively when dealing with limits and derivatives.
In this article, we’ll explore practical strategies to simplify complex algebra for L’Hôpital’s rule. You’ll learn techniques like factoring polynomials, using conjugates, and leveraging logarithmic properties to simplify rational expressions in calculus.
These steps will help your students master L’Hôpital’s rule and improve their calculus problem-solving strategies.
Let’s dive into these advanced limit evaluation methods.

Understanding the Challenges of Simplifying Algebraic Expressions
Many students find simplifying complex algebra daunting, especially when applying L’Hôpital’s rule for indeterminate forms in calculus. They often misunderstand algebraic manipulation techniques, leading to frustration and mistakes when simplifying algebra for L’Hôpital’s rule.
For instance, students struggle with polynomial factoring for L’Hôpital’s rule or recognizing common terms, which are crucial steps in simplification. Missteps in these areas can lead to incorrect limit evaluations using L’Hôpital’s rule and hinder their progress in advanced limit evaluation methods.
I’ve seen students lose confidence due to these challenges. This struggle isn’t just about solving problems; it affects their overall understanding and performance in calculus, particularly when dealing with complex fraction simplification and derivatives in L’Hôpital’s rule.
You are not alone in facing this issue, and there are effective calculus problem-solving strategies to help your students succeed in simplifying algebra for L’Hôpital’s rule.

Key Steps to Simplify Complex Algebra in L’Hôpital’s Rule
Overcoming this challenge requires a few key steps. Here are the main areas to focus on to make progress when simplifying algebra for L’Hôpital’s rule:
- Identify and factor common terms: Recognize and factor out common terms in the algebraic expressions, a crucial step in L’Hôpital’s rule explained.
- Apply algebraic manipulation techniques: Use techniques like distributing and combining like terms to simplify expressions, essential for handling indeterminate forms in calculus.
- Utilize conjugates for simplification: Apply conjugates to simplify expressions involving complex numbers, often encountered when evaluating limits using L’Hôpital’s rule.
- Rewrite expressions using log properties: Use logarithmic properties to simplify and transform expressions, a key strategy in calculus problem-solving.
- Practice substitution and cancellation: Substitute variables and cancel common terms to simplify further, particularly useful for complex fraction simplification in L’Hôpital’s rule.
- Visualize with graphing tools: Use graphing tools to see the impact of simplification steps visually, aiding in advanced limit evaluation methods.
Let’s dive in!
1: Identify and factor common terms
Identifying and factoring common terms is crucial for simplifying algebra for L’Hôpital’s rule and simplifying complex algebraic expressions in calculus problem-solving strategies.
Actionable Steps:
- Recognize common terms: Spend time practicing how to identify common terms in both the numerator and denominator of expressions when dealing with indeterminate forms in calculus.
- Factor out common terms: Use algebraic manipulation techniques or software to help factor out these terms from various sample problems involving limits using L’Hôpital’s rule.
- Verify through practice: Regularly solve problems and check your work with an algebraic expression tool to ensure accuracy in advanced limit evaluation methods.
Explanation: Recognizing and factoring common terms simplifies the process and helps avoid errors. It builds a solid foundation for more complex manipulations in simplifying rational expressions in calculus.
Practicing this skill is essential for mastering L’Hôpital’s rule explained. Using tools like Vaia’s calculus resources can provide additional practice and verification.
Key benefits of mastering this step include:
- Improved problem-solving efficiency in derivatives in L’Hôpital’s rule
- Enhanced understanding of algebraic structures for complex fraction simplification
- Reduced errors in complex calculations involving polynomial factoring for L’Hôpital’s rule
By mastering these steps, you’ll set a strong foundation for further algebraic simplification techniques in simplifying algebra for L’Hôpital’s rule.
2: Apply algebraic manipulation techniques
Applying algebraic manipulation techniques is essential for simplifying algebra for L’Hôpital’s rule and evaluating indeterminate forms in calculus.
Actionable Steps:
- Review algebraic techniques: Attend a workshop focused on advanced algebraic manipulation techniques like distributing and combining like terms, crucial for simplifying rational expressions in calculus.
- Practice with targeted problems: Complete a set of targeted practice problems to reinforce algebraic manipulation skills, including polynomial factoring for L’Hôpital’s rule.
- Use software tools: Practice manipulation using software tools like Mathematica or MATLAB to enhance your understanding of complex fraction simplification and limits using L’Hôpital’s rule.
Explanation: These steps are crucial because mastering algebraic manipulation techniques allows students to simplify expressions efficiently, leading to accurate limit evaluations and advanced limit evaluation methods.
For additional practice, resources like GeeksforGeeks provide valuable examples and explanations for L’Hôpital’s rule explained.
By focusing on these techniques, students will be better equipped to tackle complex algebraic problems in calculus and apply derivatives in L’Hôpital’s rule effectively.

3: Utilize conjugates for simplification
Utilizing conjugates can simplify expressions involving complex numbers in L’Hôpital’s rule problems, making it an essential technique for simplifying algebra for L’Hôpital’s rule.
Actionable Steps:
- Understand conjugates: Watch instructional videos to grasp how conjugates work in simplifying rational expressions in calculus.
- Practice with sample problems: Apply conjugates to a set of provided problems to reinforce your understanding of algebraic manipulation techniques for L’Hôpital’s rule.
- Seek feedback: Write step-by-step solutions using conjugates and get feedback from a mentor or tutor to improve your calculus problem-solving strategies.
Explanation: Mastering conjugates helps break down complex expressions, making them easier to handle. This method is crucial for evaluating limits correctly using L’Hôpital’s rule and dealing with indeterminate forms in calculus.
For additional guidance on simplifying algebra for L’Hôpital’s rule, check out this resource on using conjugates.
Improving these skills can significantly enhance your students’ calculus performance, especially when dealing with derivatives in L’Hôpital’s rule and advanced limit evaluation methods.
Next, let’s explore how to rewrite expressions using log properties.

4: Rewrite expressions using log properties
Rewriting expressions using log properties can significantly simplify complex algebra for L’Hôpital’s rule problems, enhancing your calculus problem-solving strategies.
Actionable Steps:
- Review logarithmic rules: Study the properties of logarithms and how they can be applied to simplify expressions, particularly when dealing with indeterminate forms in calculus.
- Practice with examples: Solve logarithmic expression problems to reinforce your understanding and skills in simplifying rational expressions in calculus.
- Use graphing calculators: Visualize the changes in expressions using graphing tools like Desmos or GeoGebra to better understand limits using L’Hôpital’s rule.
Explanation: These steps matter because they make it easier to handle complex algebraic expressions, leading to more accurate limit evaluations and advanced limit evaluation methods.
For additional practice and examples, refer to resources like GeeksforGeeks.
Understanding and applying log properties can significantly enhance your students’ ability to solve calculus problems, especially when dealing with derivatives in L’Hôpital’s rule.
Key advantages of mastering log properties include:
- Simplification of complex expressions, including complex fraction simplification
- Easier identification of limits and indeterminate forms
- Improved problem-solving speed when applying L’Hôpital’s rule
Next, let’s explore the importance of practicing substitution and cancellation techniques for simplifying algebra for L’Hôpital’s rule.

5: Practice substitution and cancellation
Practicing substitution and cancellation is crucial for simplifying algebra for L’Hôpital’s rule and mastering indeterminate forms in calculus.
Actionable Steps:
- Identify and substitute variables: Practice by identifying where substitution can simplify the expression, then replace variables accordingly when evaluating limits using L’Hôpital’s rule.
- Work through substitution exercises: Partner with a study buddy to complete substitution drills and enhance your algebraic manipulation techniques.
- Cancel common terms in fractions: Regularly practice canceling terms in complex fractions to reinforce your understanding of simplifying rational expressions in calculus.
Explanation: These steps matter because they help break down complex expressions into manageable parts, ensuring accurate limit evaluations and improving calculus problem-solving strategies.
For additional guidance on simplifying algebra for L’Hôpital’s rule, explore resources like Fiveable’s substitution techniques.
Mastering these skills will significantly improve your students’ calculus performance, especially when dealing with derivatives in L’Hôpital’s rule.
Next, let’s explore how to visualize algebraic simplification with graphing tools for advanced limit evaluation methods.

6: Visualize with graphing tools
Using graphing tools can help students understand and simplify complex algebraic expressions when applying L’Hôpital’s rule, a key technique for evaluating indeterminate forms in calculus.
Actionable Steps:
- Learn to use graphing software: Familiarize yourself with graphing tools such as Desmos or GeoGebra to visualize algebraic expressions and simplify algebra for L’Hôpital’s rule.
- Graph problems to see simplification impacts: Plot several problems to observe the effects of different simplification steps on the expressions, especially when dealing with complex fractions in calculus.
- Analyze graphs to confirm simplifications: Compare graphs before and after simplification to understand the changes and ensure accuracy when applying L’Hôpital’s rule.
Explanation: These steps are important because visualizing algebraic expressions can make complex problems more understandable and manageable, particularly when simplifying algebra for L’Hôpital’s rule.
Using graphing tools helps students see the impact of simplification, leading to more accurate limit evaluations using L’Hôpital’s rule.
For additional resources, check out this guide on innovative solutions for calculus problems.
Visualizing algebraic simplifications can significantly improve students’ comprehension and performance in calculus, especially when dealing with limits using L’Hôpital’s rule.
Benefits of using graphing tools:
- Enhanced visual understanding of expressions and derivatives in L’Hôpital’s rule
- Easier identification of function behavior in indeterminate forms
- Improved ability to verify simplification results in advanced limit evaluation methods
Next, let’s explore how Alleo can assist in mastering these techniques for simplifying algebra for L’Hôpital’s rule.

Partner with Alleo to Master Algebraic Simplification for L’Hôpital’s Rule
We’ve discussed the challenges of simplifying algebra for L’Hôpital’s rule. Did you know you can work with Alleo to make this process easier and faster?
Set up an account with Alleo and create a tailored plan for your students. Alleo’s AI coach provides affordable, personalized coaching support for simplifying algebra for L’Hôpital’s rule, just like a human coach.
With full coaching sessions on calculus problem-solving strategies and a free 14-day trial, you can explore all features without a credit card.
Alleo’s coach follows up on progress and adjusts the plan as needed. Stay accountable with reminders via text and push notifications for mastering indeterminate forms in calculus and advanced limit evaluation methods.
Ready to get started for free? Let me show you how to enhance your skills in simplifying algebra for L’Hôpital’s rule!
Step 1: Log In or Create Your Account
To get started with Alleo’s AI coach for mastering algebraic simplification in L’Hôpital’s rule, Log in to your account or create a new one to access personalized coaching support.

Step 2: Choose Your Focus – Building Better Habits and Routines
Click on “Building better habits and routines” to start developing consistent practices for simplifying complex algebra, which will help you master L’Hôpital’s rule and improve your overall calculus performance.

Step 3: Select “Career” as Your Focus Area
Choose “Career” as your focus area to enhance your algebraic skills for L’Hôpital’s rule, directly improving your teaching effectiveness and advancing your professional development in mathematics education.

Step 4: Starting a coaching session
Begin your journey with Alleo by participating in an intake session, where you’ll discuss your algebra simplification challenges and set up a personalized plan to improve your L’Hôpital’s rule application skills.

Step 5: Viewing and Managing Goals After the Session
After your coaching session on simplifying algebra for L’Hôpital’s rule, check the app’s home page to view and manage the goals you discussed, allowing you to track your progress and stay focused on improving your calculus skills.
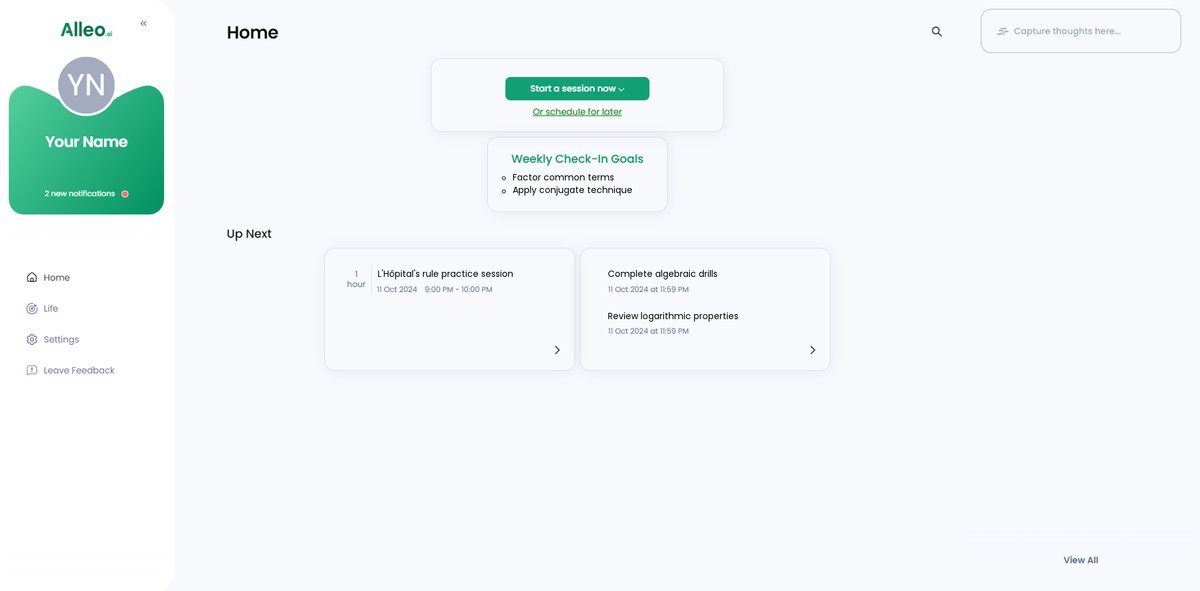
Step 6: Adding events to your calendar or app
Track your progress in simplifying complex algebra for L’Hôpital’s rule by adding practice sessions and milestones to your calendar or task list in the Alleo app, helping you stay organized and motivated throughout your learning journey.
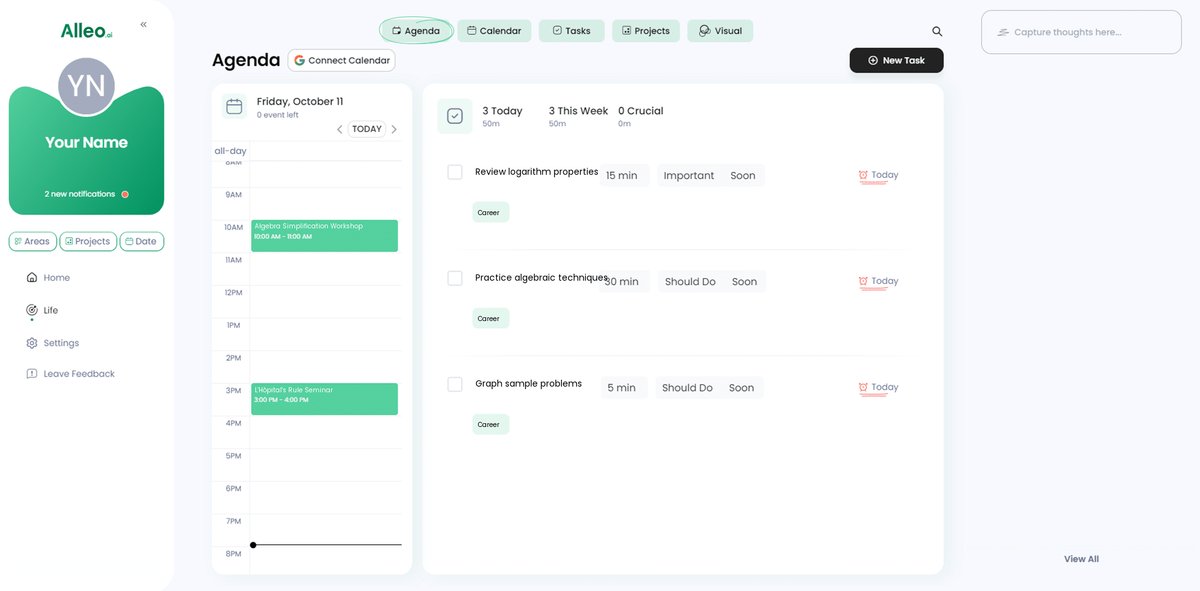
Wrapping Up: Simplifying Algebra for L’Hôpital’s Rule
We’ve covered how to simplify complex algebraic expressions for L’Hôpital’s rule. These strategies for simplifying algebra for L’Hôpital’s rule will make a significant difference in your students’ calculus journey.
By focusing on recognizing common terms, applying algebraic manipulation techniques, and using conjugates, your students can master this challenging topic and excel in evaluating limits using L’Hôpital’s rule.
Incorporating log properties, practicing substitution, and visualizing with graphing tools will further enhance their skills in dealing with indeterminate forms in calculus and advanced limit evaluation methods.
I understand the frustration that comes with these challenges in simplifying rational expressions in calculus. You’re not alone, and with consistent practice of calculus problem-solving strategies, progress will follow.
Consider trying Alleo’s personalized coaching to support your students in mastering L’Hôpital’s rule explained. Sign up for a free 14-day trial and see the difference for yourself.